-
Table of Contents
Z TEST SAMPLE PROBLEMS WITH SOLUTION PPT
When it comes to statistical analysis, the Z-test is a powerful tool used to determine whether there is a significant difference between a sample mean and a population mean. In this article, we will explore Z test sample problems with solutions in a PowerPoint presentation format. By the end of this article, you will have a clear understanding of how to solve Z test sample problems and present your findings effectively.
Understanding the Z Test
The Z-test is a statistical test that is used to determine whether the mean of a sample is significantly different from the mean of a population. It is based on the standard normal distribution and is commonly used when the sample size is large (typically n > 30) or when the population standard deviation is known.
Key Concepts of the Z Test
- Z Score: The Z score is a measure of how many standard deviations a data point is from the mean of a distribution. It is calculated using the formula Z = (X – μ) / σ, where X is the sample mean, μ is the population mean, and σ is the population standard deviation.
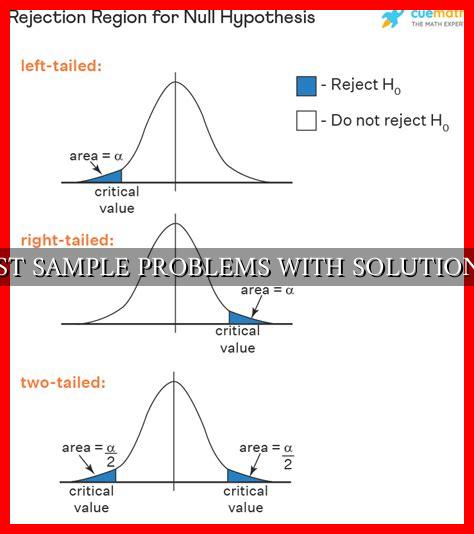
- Null Hypothesis: The null hypothesis in a Z test states that there is no significant difference between the sample mean and the population mean.
- Alternative Hypothesis: The alternative hypothesis in a Z test states that there is a significant difference between the sample mean and the population mean.
Z Test Sample Problems
Let’s consider a sample problem to illustrate how the Z test is applied in practice:
Problem: A manufacturer claims that the average weight of their product is 500 grams.
. A random sample of 50 products is taken, and the average weight is found to be 490 grams with a standard deviation of 10 grams. Test the manufacturer’s claim at a significance level of 0.05.
Solution
To solve this problem, we need to follow these steps:
- State the null and alternative hypotheses:
- Null Hypothesis (H0): μ = 500 grams
- Alternative Hypothesis (Ha): μ ≠ 500 grams
- Calculate the Z score using the formula Z = (X – μ) / (σ / √n), where X = 490 grams, μ = 500 grams, σ = 10 grams, and n = 50.
- Compare the calculated Z score with the critical Z value at a significance level of 0.05.
- Make a decision to reject or fail to reject the null hypothesis based on the comparison.
Presenting Z Test Results in a PowerPoint Presentation
When presenting Z test results in a PowerPoint presentation, it is essential to create a clear and visually appealing slide deck. Here are some tips for creating an effective presentation:
- Use clear and concise language to explain the problem and the steps taken to solve it.
- Include visuals such as graphs or charts to illustrate the data and results.
- Highlight key findings and conclusions to make them stand out to the audience.
- Provide references or external links for further reading on the topic.
Conclusion
In conclusion, Z test sample problems with solutions in a PowerPoint presentation format can help you understand and apply statistical concepts effectively. By following the steps outlined in this article and presenting your findings clearly, you can make informed decisions based on data analysis. Remember to practice solving Z test problems and creating presentations to enhance your statistical skills.
For more information on Z tests and statistical analysis, you can refer to this external link.