-
Table of Contents
The Unit Circle: What Is It?
When it comes to trigonometry, the unit circle is a fundamental concept that plays a crucial role in understanding the relationships between angles and trigonometric functions. In this article, we will delve into what the unit circle is, why it is important, and how it can be used to solve trigonometric problems.
What is the Unit Circle?
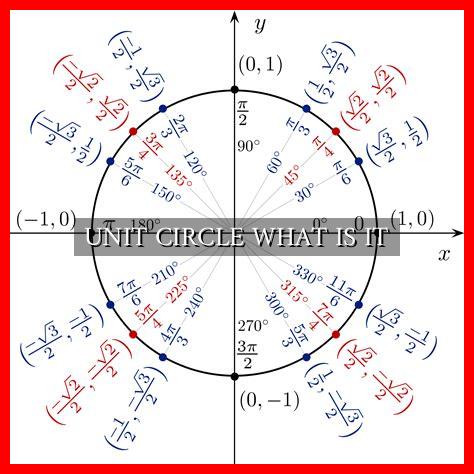
The unit circle is a circle with a radius of 1 unit, centered at the origin of a coordinate plane. It is divided into four quadrants, each representing a different range of angles. The unit circle is a powerful tool in trigonometry because it allows us to easily visualize the values of trigonometric functions for different angles.
Why is the Unit Circle Important?
The unit circle provides a way to relate the values of sine, cosine, and tangent to the coordinates of points on the circle. By understanding the properties of the unit circle, we can simplify trigonometric calculations and solve complex problems more efficiently.
How to Use the Unit Circle
One of the key concepts in using the unit circle is understanding the relationship between angles and trigonometric functions.
. For example, the coordinates of a point on the unit circle at an angle θ are given by (cos θ, sin θ). This relationship allows us to easily determine the values of sine and cosine for any angle on the unit circle.
- For example, at an angle of 30 degrees (π/6 radians), the coordinates of the point on the unit circle are (√3/2, 1/2). This means that sin(30°) = 1/2 and cos(30°) = √3/2.
- Similarly, at an angle of 45 degrees (π/4 radians), the coordinates are (√2/2, √2/2), leading to sin(45°) = √2/2 and cos(45°) = √2/2.
Applications of the Unit Circle
The unit circle is used in various fields such as physics, engineering, and mathematics to solve problems involving periodic functions, oscillations, and waveforms. Understanding the unit circle can help in analyzing the behavior of these functions and making predictions based on their properties.
For example, in physics, the unit circle is used to study the motion of objects in circular or oscillatory patterns. By applying trigonometric functions to the coordinates of points on the unit circle, physicists can accurately describe the motion of these objects and predict their future positions.
Conclusion
In conclusion, the unit circle is a powerful tool in trigonometry that allows us to visualize the relationships between angles and trigonometric functions. By understanding the properties of the unit circle and how to use it effectively, we can simplify complex trigonometric calculations and solve problems more efficiently. Whether you are a student learning trigonometry or a professional working in a related field, mastering the unit circle can greatly enhance your understanding of trigonometric concepts and their applications.
For more information on the unit circle and its applications, you can visit Khan Academy’s Unit Circle Trigonometry page.