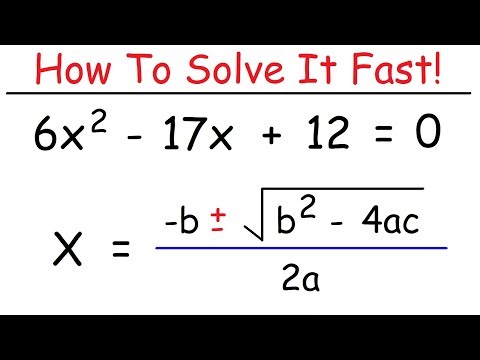-
Table of Contents
Solutions for Quadratic Equations
Quadratic equations are a fundamental concept in algebra that involve a polynomial equation of the form ax^2 + bx + c = 0, where a, b, and c are constants. Finding solutions to quadratic equations is a common task in mathematics and has numerous real-world applications. In this article, we will explore various methods and techniques for solving quadratic equations.
1. Factoring
One of the most common methods for solving quadratic equations is factoring. This method involves rewriting the quadratic equation in the form of two binomials that multiply to the original equation. For example, consider the quadratic equation x^2 + 5x + 6 = 0. By factoring, we can rewrite this equation as (x + 2)(x + 3) = 0. Setting each binomial equal to zero gives us the solutions x = -2 and x = -3.
2. Quadratic Formula
Another popular method for solving quadratic equations is using the quadratic formula. The quadratic formula states that for any quadratic equation ax^2 + bx + c = 0, the solutions are given by x = (-b ± √(b^2 – 4ac)) / 2a. This formula provides a straightforward way to find the roots of a quadratic equation, even when factoring is not possible.
3. Completing the Square
Completing the square is another method for solving quadratic equations that involves rewriting the equation in a perfect square trinomial form. By adding and subtracting a constant term to make the quadratic expression a perfect square, we can easily find the solutions to the equation. This method is particularly useful for equations that are not easily factorable.
4. Graphical Method
Graphing quadratic equations can also help in finding solutions. By plotting the quadratic function on a graph, the x-intercepts of the graph represent the solutions to the quadratic equation. This method is visually intuitive and can provide a quick way to verify the solutions obtained through other methods.
5. Applications in Real Life
Quadratic equations have numerous applications in real life, such as in physics, engineering, economics, and computer science. For example, in physics, quadratic equations are used to model the motion of objects under the influence of gravity. In economics, quadratic equations can be used to optimize production costs or revenue. Understanding how to solve quadratic equations is essential for tackling these real-world problems.
Conclusion
Solving quadratic equations is a fundamental skill in mathematics with a wide range of applications. By mastering various methods such as factoring, using the quadratic formula, completing the square, and graphing, one can efficiently find solutions to quadratic equations. Whether in academic settings or real-world scenarios, the ability to solve quadratic equations is a valuable tool that can lead to deeper insights and problem-solving skills.