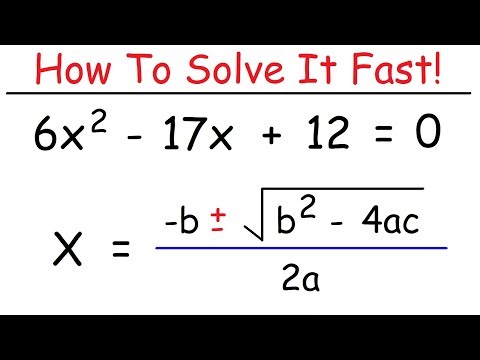-
Table of Contents
QUADRATIC FORMULA PRACTICE PROBLEMS WITH ANSWERS
Quadratic equations are a fundamental concept in algebra, and mastering the quadratic formula is essential for solving these equations efficiently. Practice problems are a great way to reinforce your understanding of the quadratic formula and improve your problem-solving skills. In this article, we will provide you with a variety of quadratic formula practice problems along with detailed solutions to help you sharpen your math skills.
Understanding the Quadratic Formula
The quadratic formula is used to solve quadratic equations of the form ax^2 + bx + c = 0, where a, b, and c are constants and a ≠ 0. The quadratic formula is given by:
x = (-b ± √(b^2 – 4ac)) / 2a
By substituting the values of a, b, and c into the formula, you can find the solutions (roots) of the quadratic equation. The ± symbol indicates that there are usually two solutions to a quadratic equation.
Practice Problems
Let’s dive into some quadratic formula practice problems to test your understanding:
Problem 1:
Solve the quadratic equation x^2 – 5x + 6 = 0.
Solution:
- a = 1, b = -5, c = 6
- Substitute the values into the quadratic formula:
x = (5 ± √(25 – 24)) / 2
Therefore, the solutions are x = 2 and x = 3.
Problem 2:
Find the roots of the equation 2x^2 + 3x – 2 = 0.
Solution:
- a = 2, b = 3, c = -2
- Substitute the values into the quadratic formula:
x = (-3 ± √(9 + 16)) / 4
Thus, the solutions are x = -2 and x = 1/2.
Additional Resources
If you want to practice more quadratic formula problems, you can visit Math is Fun for a wide range of practice questions with answers.
Summary
In conclusion, mastering the quadratic formula is crucial for solving quadratic equations efficiently.
. By practicing a variety of problems, you can enhance your problem-solving skills and gain confidence in tackling complex algebraic equations. Remember to substitute the values of a, b, and c correctly into the formula and pay attention to the ± symbol to find both solutions. Keep practicing, and you’ll soon become a pro at solving quadratic equations!