-
Table of Contents
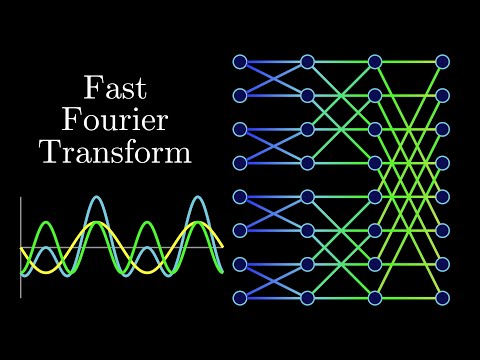
High-Speed Fourier Transform Algorithm Optimized for Electronics
Fourier Transform is a mathematical technique that transforms a signal from the time domain to the frequency domain. It is widely used in various fields such as signal processing, image processing, and telecommunications. In the realm of electronics, the Fourier Transform plays a crucial role in analyzing and processing signals. However, traditional Fourier Transform algorithms can be computationally intensive and time-consuming, especially when dealing with large datasets. This has led to the development of high-speed Fourier Transform algorithms optimized for electronics.
The Need for High-Speed Fourier Transform Algorithms
With the increasing complexity of electronic systems and the growing demand for real-time signal processing, there is a need for high-speed Fourier Transform algorithms that can efficiently handle large amounts of data.
. Traditional algorithms such as the Fast Fourier Transform (FFT) have limitations when it comes to processing signals in real-time or dealing with high-resolution data. This has spurred research into developing optimized algorithms that can meet the requirements of modern electronics.
Optimizations for Electronics
Researchers have been working on optimizing Fourier Transform algorithms specifically for electronic applications. These optimizations aim to reduce computational complexity, improve speed, and enhance efficiency. Some of the key optimizations include:
- Parallel processing: Utilizing multiple processing units to perform computations simultaneously, speeding up the Fourier Transform process.
- Hardware acceleration: Implementing specialized hardware such as Field-Programmable Gate Arrays (FPGAs) or Graphics Processing Units (GPUs) to offload computational tasks and improve performance.
- Algorithmic improvements: Developing new algorithms or modifying existing ones to reduce the number of operations required for the Fourier Transform.
Case Study: Optimized Fourier Transform for Radar Systems
One example of the application of high-speed Fourier Transform algorithms in electronics is in radar systems. Radar systems require fast and accurate signal processing to detect and track targets. By using optimized Fourier Transform algorithms, radar systems can achieve real-time processing of radar signals, enabling quick decision-making and target identification.
Researchers at MIT have developed a high-speed Fourier Transform algorithm specifically tailored for radar systems. This algorithm leverages parallel processing and hardware acceleration to achieve significant speed improvements compared to traditional FFT algorithms. The optimized algorithm has been successfully implemented in radar systems, demonstrating its effectiveness in real-world applications.
Benefits of High-Speed Fourier Transform Algorithms
The use of high-speed Fourier Transform algorithms optimized for electronics offers several benefits:
- Improved processing speed: High-speed algorithms can process signals faster, enabling real-time applications.
- Reduced computational complexity: Optimizations help reduce the computational burden, making it easier to handle large datasets.
- Enhanced efficiency: By utilizing parallel processing and hardware acceleration, algorithms can achieve higher efficiency in signal processing tasks.
Conclusion
In conclusion, high-speed Fourier Transform algorithms optimized for electronics play a crucial role in enabling fast and efficient signal processing in modern electronic systems. By leveraging parallel processing, hardware acceleration, and algorithmic improvements, these optimized algorithms offer significant speed improvements and efficiency gains. As electronic systems continue to advance in complexity and performance requirements, the development of high-speed Fourier Transform algorithms will be essential in meeting the demands of the industry.